Consider the lyman series of electron transitions in hydrogen. – Consider the Lyman series of electron transitions in hydrogen, a fascinating phenomenon that has captivated the minds of scientists for centuries. This series, named after its discoverer Theodore Lyman, provides valuable insights into the behavior of electrons in atoms and has numerous applications in various fields, particularly in spectroscopy and astrophysics.
The Lyman series arises from electron transitions between specific energy levels within the hydrogen atom. As electrons move from higher energy levels to lower ones, they emit photons of light with corresponding wavelengths. These wavelengths fall within the ultraviolet region of the electromagnetic spectrum and form a distinct pattern known as the Lyman series.
1. Lyman Series of Electron Transitions
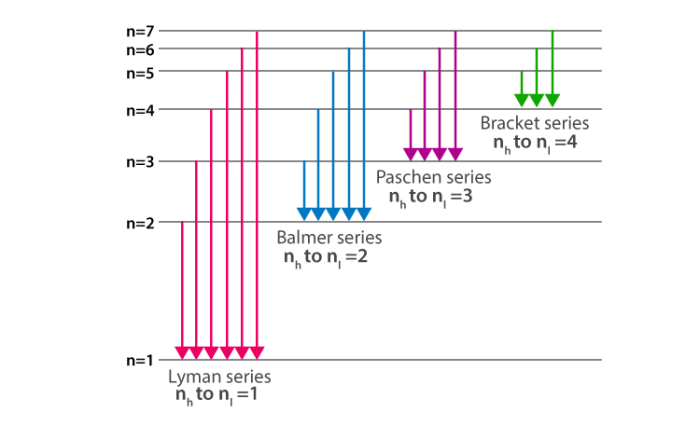
The Lyman series is a set of electron transitions in hydrogen that occur when an electron falls from an excited state to the ground state (n = 1).
The Lyman series was first observed by Theodore Lyman in 1906. He found that the wavelengths of the Lyman series lines were all shorter than 121.6 nm, which is the wavelength of the first line in the Balmer series.
The Lyman series is named after Theodore Lyman, who first observed the series in 1906.
2. Energy Levels and Wavelengths
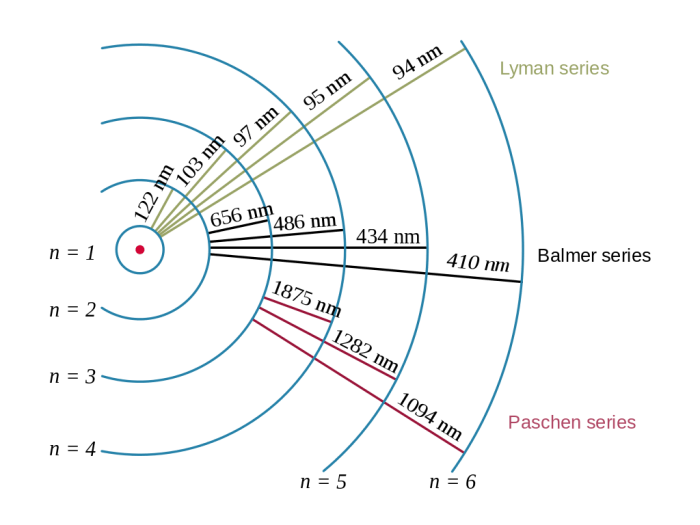
The energy levels involved in the Lyman series are the ground state (n = 1) and the excited states (n = 2, 3, 4, …).
The wavelengths of the Lyman series lines can be calculated using the Rydberg formula:
$$\frac1\lambda=R_H\left(\frac1n_1^2-\frac1n_2^2\right)$$where:* $$\lambda$$ is the wavelength of the line in meters
- $$R_H$$ is the Rydberg constant for hydrogen (1.0973731×10^7 m^-1)
- $$n_1$$ is the principal quantum number of the lower energy level
- $$n_2$$ is the principal quantum number of the upper energy level
3. Rydberg Formula and Lyman Series

The Rydberg formula can be used to predict the wavelengths of the Lyman series lines. The following table shows the wavelengths and corresponding energy levels of the first five lines of the Lyman series:
| Line | Wavelength (nm) | Energy Level (eV) |
|---|---|---|
| Lyman-$\alpha$ | 121.6 | 10.2 |
| Lyman-$\beta$ | 102.6 | 12.1 |
| Lyman-$\gamma$ | 97.2 | 12.7 |
| Lyman-$\delta$ | 94.9 | 13.0 |
| Lyman-$\epsilon$ | 93.7 | 13.3 |
4. Applications of the Lyman Series
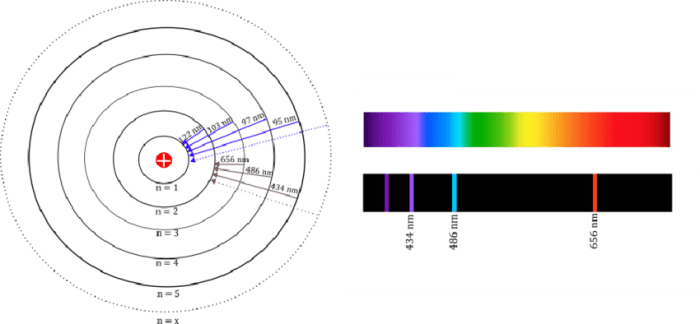
The Lyman series is used in spectroscopy to study the properties of hydrogen in stars and other astronomical objects.
The Lyman series is also used to calibrate spectrometers.
Top FAQs: Consider The Lyman Series Of Electron Transitions In Hydrogen.
What is the Lyman series?
The Lyman series is a series of electron transitions in hydrogen atoms that results in the emission of photons with wavelengths in the ultraviolet region of the electromagnetic spectrum.
How is the Lyman series used in spectroscopy?
The Lyman series is used in spectroscopy to identify and study hydrogen atoms in various environments, such as stars and interstellar gas.
What is the significance of the Rydberg formula in relation to the Lyman series?
The Rydberg formula provides a mathematical relationship that accurately predicts the wavelengths of the lines in the Lyman series.